Sin conocerlo, el mundo financiero puede parecer tan o más difícil que aprender caracteres chinos. CDS, MBS, CD, LBO, etcétera…
Muchas son abreviaciones de cosas tan sencillas como un depósito bancario en el caso de CD (Certificate of Deposit), y muchas otras son abreviaciones de cosas que pueden parecer complicadas, y que no tienen traducción, como el CDS (Credit Default Swap).
En este post voy a hacer una rápida y sencilla explicación sobre una de las grandes categorías de productos financieros, la renta fija.
El bono
Imaginate que le prestas 1,000 EUR a tu suegro y te dice que te lo va a devolver de golpe en un año, pero como es el padre de tu pareja y no quieres problemas en casa, no le cobrarás ningún interés.
Hoy, a 1 de Enero del año 1, le das dos billetes de 500 EUR y él, para formalizar la deuda, te firma un papelito donde se compromete a pagarte los 1.000 el día 1 de enero del año 2 para cumplir con su deuda.
Al cabo de un año, tu le devuelves el papelito firmado y el te da los 1,000 EUR de vuelta. Hasta ahí, todo correcto. Para aclararlo más podemos hacer una línea temporal, donde lo que pagamos va debajo de la línea en rojo y en negativo, y lo que recibimos arriba en negro y positivo.
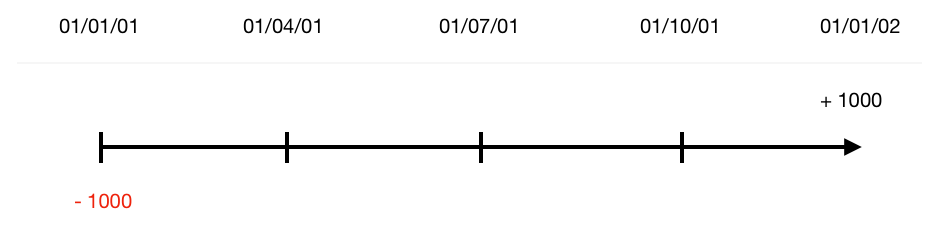
Imagínate ahora, que cambiamos tu suegro por una empresa. Mismas condiciones, 1,000 EUR ahora por 1,000 EUR dentro de un año (de momento digamos que somos tan chulos que prestamos el dinero gratis).
El papelito que te firma la empresa comprometiéndose a pagarte 1,000 EUR en un año se llama bono.
En la vida real, nunca prestaríamos dinero gratuitamente, así que lo que va a ocurrir será lo siguiente: La empresa, que se llama “XYZ”, va a venir y nos va a preguntar cuánto estamos dispuestos a pagarle por un bono que paga 1,000 EUR en un año.
Nosotros, teniendo en cuenta el riesgo que hay de que la empresa no pague y el hecho de que no podremos disponer del dinero durante un año, le ofrecemos darle 900 EUR hoy por un pago de vuelta de 1,000 el año que viene.
XYZ acepta, pagamos, y recibimos el bono. En un año, le devolvemos el bono a la empresa, nos paga los 1,000 EUR, y nos vamos contentos por qué hemos ganado 100 EUR, lo que es un 11.1% sobre nuestra inversión inicial de 900 EUR.
Este bono, lo llamaríamos un bono con cupón 0 (o sin cupón) a un año. Y ahora vas a pensar: “lo del año vale, pero ¿y lo del cupón?” No te preocupes, más adelante verás que es esto del cupón.
Antes de continuar, me gustaría hacer dos aclaraciones.
La primera aclaración es que una empresa puede emitir bonos, pero los estados y administraciones públicas también. Por poner un ejemplo, la ciudad de Chicago emite bonos para financiar proyectos. Y más conocidos son para los europeos los fabulosos bonos de deuda española, italiana y griega.
La segunda aclaración es que el vencimiento de un bono (el vencimiento es la fecha en la que te pagan) puede ser en un día o en décadas. Puede haber vencimientos en 15, 20, o 30 años. Hay que decir que cuando son bonos de tan largo plazo normalmente es deuda soberana (bonos emitidos por estados).
También es importante saber que siempre que hablamos de intereses, lo hacemos con intereses anuales, sea una deuda de 1 año, de 6 meses o de 20 años. El tipo de interés siempre se anualiza.
Bonos con cupón
Retomemos el ejemplo de la empresa XYZ. Al ir tan bien la primera vez que emitieron un bono, lo quieren hacer de nuevo, pero ahora un poco distinto. Ahora nos van a preguntar cuanto estaríamos dispuestos a pagar hoy por un bono que paga 1,000 EUR en 1 año exacto y que cada trimestre nos da 50 EUR, incluido el último, de forma que si dibujamos una línea temporal nos quedaría de la siguiente manera:
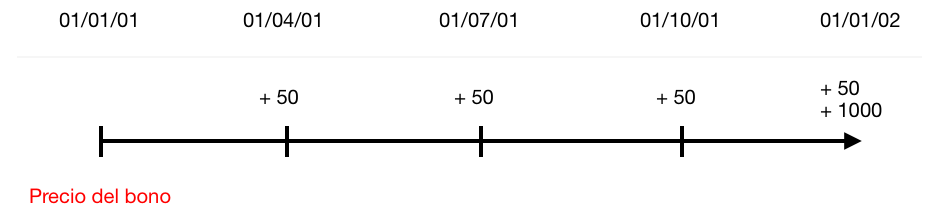
Estos pagos de 50 EUR se llaman cupones, y los 1,000 EUR del pago final se llaman principal. A este bono lo llamaríamos un bono de XYZ con un principal de 1,000, vencimiento de 1 año y un cupón trimestral de 50 EUR o del 5% (porcentaje con respecto al principal).
Tasa de descuento
Para poder determinar el valor del bono tenemos que calcular primero cuánto estamos dispuestos a dar hoy para que nos devuelvan 50 EUR en 3, 6, 9, y 12 meses.
La suma de estos valores junto con el valor de un pago de 1,000 EUR en un año, que sabemos por el precio del primer bono que es de 900 EUR, nos dará el valor del bono a día de hoy.
A este proceso se le llama descontar, y es el proceso por el cual determinamos el valor actual de una serie de pagos hechos en un futuro.
Para poder realizarlo, necesitamos saber la tasa de descuento, que en el caso nuestro bono era de 11.1%. En futuros artículos veremos cómo intuirla, pero por hoy simplemente hay que saber que es el porcentaje al que un pago futuro va perdiendo valor actual a medida que se hace mas tarde.
Por ejemplo, en el caso del bono sin cupón, el inversor era indiferente entre recibir 900 EUR hoy y recibir 1,000 en 1 año. 900 es un 11.1% más bajo que 1.000, por lo que 11.1 % es la tasa anual de descuento.
Si descontamos un 11.1% de 900, nos daría 810.08. Esto significaría que un pago de 1.000 EUR en 2 años seria equivalente a un pago de 900 EUR en un año, y a un pago de 810.08 EUR ahora.
Si intentamos hacer deducciones, nos daremos cuenta que cuanto más tiempo descontemos un pago, menos valor tendrá. Lógicamente, preferimos que nos paguen 100 EUR en un año a que nos paguen 100 EUR en 10 años, es decir, el mismo pago tiene más valor para nosotros si es en 1 año que en 10.
Valoración de un bono
Explicada la tasa de descuento, veamos como quedan los cupones del segundo bono descontados:
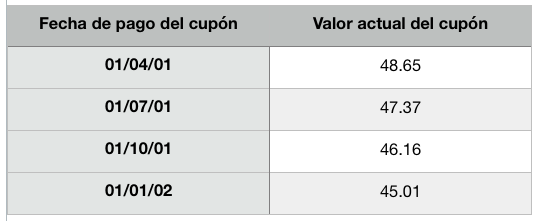
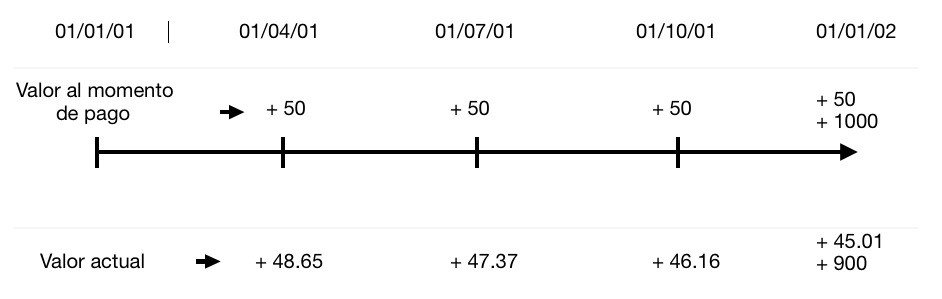
El valor del bono simplemente es la suma del valor actual de todos los cupones y del principal. En este caso sería 48.65 + 47.37 + 46.16 + 45.01 + 900, y nos da un resultado de 1,087.19 EUR.
Este es el valor del bono, ya que para ti (el inversor) es indiferente recibir 1087.19 EUR hoy que la serie de pagos que representa el bono. Seguidamente puedes ver representados los pagos del bono con su valor descontado en una linea del tiempo:
Para los curiosos, la fórmula que estamos usando para descontar pagos futuros es la siguiente:
PV = FV / (1 + i)t
Donde “PV” es el valor actual (del inglés Present Value); “FV” es el valor nominal del pago futuro (del inglés Future Value); “i” es la tasa de descuento (en tanto por uno y anualizada), y “t” es el numero de años que estamos descontando
Variaciones en la tasa de descuento
Como ya he dicho, en este articulo no voy a explicar ni cómo ni porqué puede variar la tasa de descuento ya que me alargaría demasiado. En cualquier caso hay que tener en mente que puede variar.
En el caso del ejemplo, la tasa de descuento era del 11.1% simplemente porque es la que yo he puesto en el ejemplo que me he inventado. En bonos de empresas o estados solventes la tasa de descuento suele estar entre el 1% y el 4%.
Si nuestro bono estuviera valorado con una tasa de descuento del 2% tendríamos que recalcular el valor actual de todos los pagos futuros con la nueva tasa. La línea temporal quedaría de la siguiente manera:
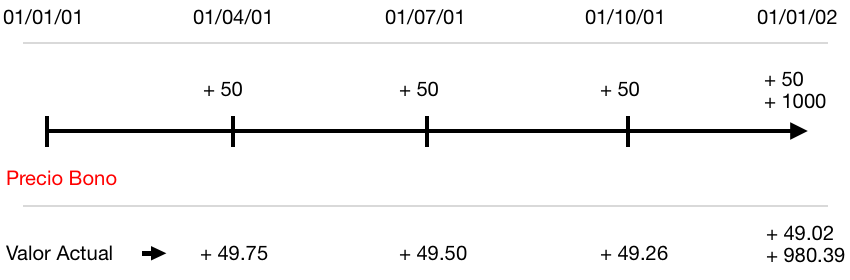
El precio del bono con una tasa anual de descuento del 2% es la suma de los valores actuales de los cupones y el principal: 49.75 + 49.50 + 49.26 + 49.02 + 980.39 = 1,177.92 EUR.
Podemos ver que el precio es más alto, ya que antes el precio era de 1,087.19. Podemos deducir que cuanto más alta sea la tasa de descuento, más bajo será el valor que le daremos a un pago futuro.
Aquí acaba esta breve introducción a la renta fija, y su máximo exponente, el bono. En caso de que tengas dudas o quieras que hable sobre un tema en concreto, puedes usar la caja de comentarios que está justo debajo y miraré de resolver las dudas.
